平面四杆机构设计

图解法

设计的基本思想
对于四杆机构来说，当其较链中心位置确定后，各杆的长度也就确定了.用作图法设计四杆机构，就是利用各较链之间相对运动的几何关系，通过作图确定各较链的位置，从而定出各杆的长度。

四杆机构图解设计的实质：用作图法确定各较链中心的位置的问题

中垂线原理：

连杆的运行时是圆周摆动，通过三点两线的中垂线可以相交得到连杆旋转的圆心。

例题1：已知活动较链B、C的3个位置，确定固定较链A、D位置。作图依据: A、D分别为B、C所在轨迹圆弧的圆心。

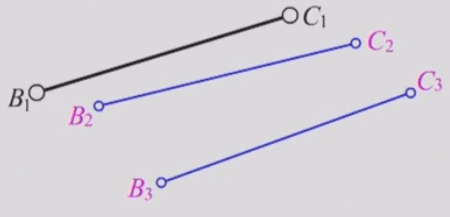
作图方法:
1）分别作连线B1B2和B2B3 的中垂线b12、b23,其交点即为A的位置;

2）同理可求D的位置;连接AB1、C1D，即得所求四杆机构AB1CiD。

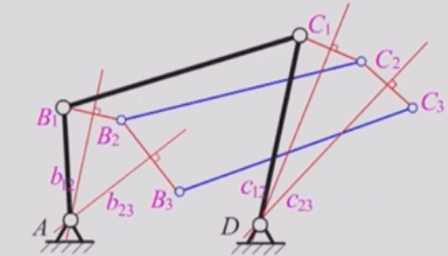
机构倒置原理：

已知固定较链A、D 位置，确定活动较链B、C 位置机构倒置原理: 若改取机构的原连杆BC为机架，原机架AD为连杆,则A、D就变为活动饺链，而B、C变为固定较链了。

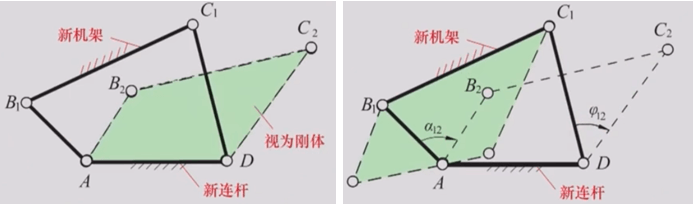
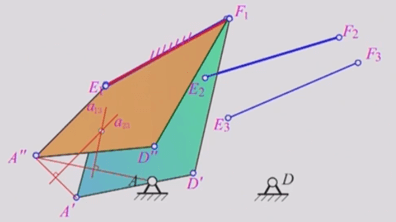
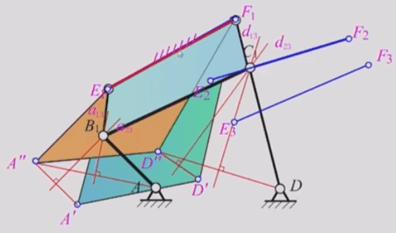
例题2：已知固定较链A、D 位置。设已知A、D 的位置，及连杆上的标线EF 在机构运动过程中，分别占据E1F1、E2F2、E3F3三个位置。现要求确定两活动较链中心B、C的位置。

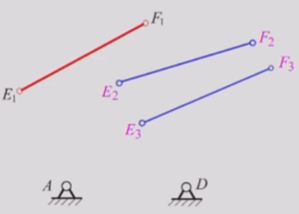
作图方法:
1)以EiFi为机架作机构倒置，作出4、D另外两个位置4、D及A”、D”

2)由4、4、A”三点确定圆弧的圆心Bi点，D、D、D”可求得Ci点

3)连接AB1、BC及CD，即得所求四杆机构ABiCiD。

按给定连杆预定N位置设计四杆机构的求解条件

当N=3 时，有唯一解;

当N=2 时，有无穷多解。此时可根据其他条件选定一个解;

当N=4 时，可能有解或无解，若重选B;位置，可能有无穷多解

反转法原理：

取机构原连架杆CD为机架，则连架杆AB变为连杆，进行机构倒置。这样，将原求活动饺链C的位置问题转化为求固定饺链C的问题。这种方法称为反转法或机构反转法

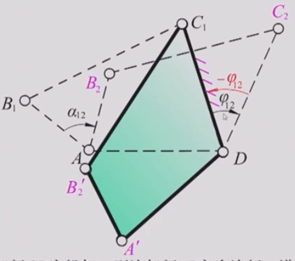
例题3：已知两连架杆两对对应角位移

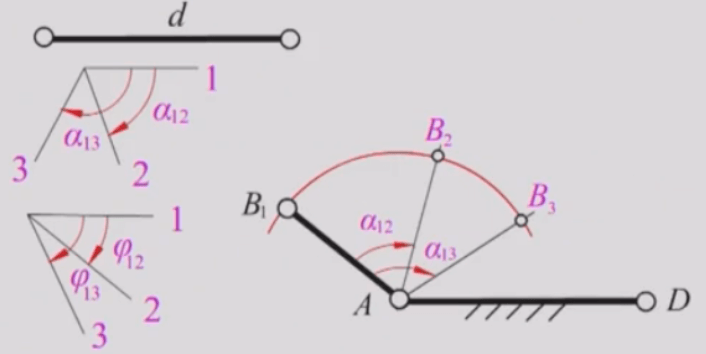
作图方法:

1)先由d 定出位置A、D，适当取AB长度及位置AB1，作位置AB2、AB3;

2)为确定C，采用反转法原理，作连线B2D 及B3D，并分别绕D点反转φ12及-φ13角，可得B2’及B3’;

3)由B1、B及B;确定C1位置。

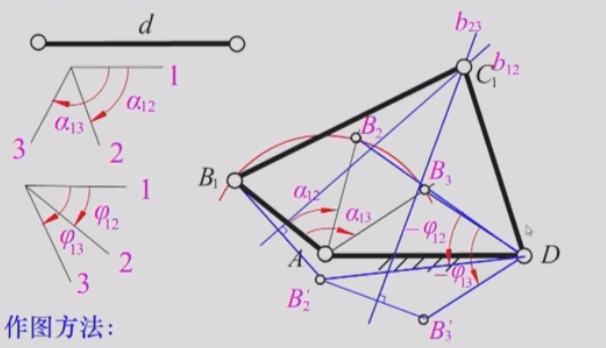
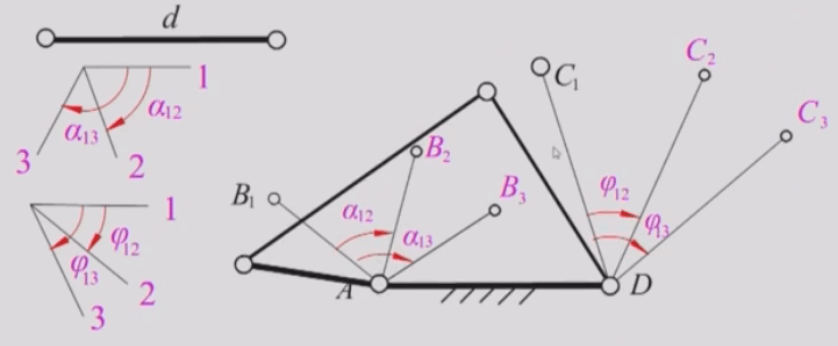
当已知两连架杆两对对应角位移时，因杆AB的长度及其初始位置AB为任选，故有无穷多解。

解析法

在用解析法设计四杆机构时，首先需建立包含机构各尺度参数和运动变量在内的解析式，然后根据已知的运动变量求机构的尺度参数。

方法特点 :
可借助于计算器或计算机求解，计算精度高，适应于对三个或三个以上位置设计的求解，尤其是对机构进行优化设计和精度分析十分有利。